Introduction
The entirety of the original post about the Theoputer ALU was dedicated to describing addition. But the curious reader may have wondered why subtraction is mentioned suspiciously sparingly, despite it being a critical operation. Indeed even the very first Theoputer ALU included subtraction. It turns out to be pretty hard (I think theoretically impossible if my Computation Theory coursework is getting recalled correctly) to build a Turing Complete machine without it.
Ok, subtraction is important, but it turns out to be so elegantly implementable thanks to a clever invention known as two’s complement numbers. We could just jump to the details and the formulas, but that won’t give us much help if we encounter issues down the road where we need to debug things. You can certainly cut to the proverbial chase and read the Wikipedia article on two’s complement numbers. But cutting to the chase sort of belies the whole point of this blog.
Who’s Compliment?
Abandon what you know about two’s complement numbers. Let’s do this from very basic arithmetic principles. Let’s start by considering negative numbers in our familiar decimal system. After all, subtraction is really just addition if you have negative numbers around. And you can’t “get” to the negative numbers from the positive numbers unless subtraction is allowed, so the concept of negative numbers and subtraction are clearly linked.
In everyday decimal, we kind of cheat when it comes to negative numbers. We just stick a ‘-’ symbol in front of a number to “make it negative”. And that’s convenient because we use the same symbol to indicate the operation of subtraction. In binary, and especially in a computer, we can’t use the same strategy because a symbol just tells us what to do; it doesn’t adjust the process of addition to become subtraction. In theory we could look for this symbol, or hold on to it alongside the 8bit numbers, and change the process to be one of subtraction. But that would require adding another bit anyway. A kind of yes/no flag that the ALU would have to look at to take path ‘subtraction’ versus path ‘addition’.
A naive approach would be to just tack on the negative/non-negative bit at the highest order location. Since we don’t want to redesign our entire computer to be a 9bit machine, we could do something like:
$$ [s,b_6,b_5,b_4,b_3,b_2,b_1,b_0] $$Note: I’m using 0-based indexing here for reasons that will be convenient later.
Where \(s\) would denote the “sign” of the number. That certainly would allow us to represent negative numbers, but what does it mean for being able to perform subtraction? It means nothing on the surface. At least not unless by some weird chance adding numbers that have this flag set/not set results in subtraction. We will see in a bit (pun intended) that this does not work. However, it turns out there is a very clever way to take this same idea and make it so that we can perform the same kind of addition that happens in a traditional ALU (via the Full Adders) and get a subtraction result instead!
Aside: I think it’s hard to appreciate how someone could come up with the following scheme. Often I read about two’s complement and I understand it, but I don’t really understand how someone thought of it. So I’m going to take you through how to understand two’s complement so that we can apply the same creativity when we encounter problems for which there isn’t a solution.
A Naive Approach
Let’s start from simple principles and build up. Ideally we want to be able to do the following:
$$ c = b + a $$Where \(a\), \(b\), and \(c\) are all numbers that can be negative. Subtraction could then be easily implemented by first turning \(a\) into negative \(a\) and then running negative \(a\) and \(b\) through our adder. Recall our process for adding together numbers:
- Add the least-significant digits
- Carry over any amount above the digit limit to the next-significant digit
- Add the next significant digits and the carry
- Go to step 2 and repeat until out of digits
Let’s see if that works with the simple approach of using the most-significant bit for the sign. Let’s try adding \(1011_2 + 0011_2 = -3 + 3\). We expect to get zero as an answer. Let’s see:
1 0 1[1]
0 0 1[1]
-----------
0
(carry=1)
[1] (carry)
1 0[1]1
0 0[1]1
-----------
1 0
(carry=1)
[1] (carry)
1[0]1 1
0[0]1 1
-----------
1 1 0
(carry=0)
[0] (carry)
[1]0 1 1
[0]0 1 1
-----------
1 1 1 0
(carry=0)
We got \(1110_2 = -6\). Uh oh. Let’s think more fundamentally about this. The more fundamental we can think about a problem, the better we can understand it and find good solutions. Einstein was famous for this ability. And if it was good enough for him, it’s good enough for us.
Back to Some Base-ics
Let’s consider what a binary number really is. It’s just a series of weights or coefficients on a set of base values. That’s a bit jargon-y, but what it means for us is two things in our binary number system:
- We have two possible weights, or values we can assign to each digit: $1$ and $0$
- Each successive digit requires us to add a new base, and that base is a power of $2$.
This is where binary gets its official name “base 2”. The reason for (1) is one of those “true by definition” things. We are calling this number system base-2 or binary, which means by definition we are only allowing two options for the digit values. Conclusion (2) is a little more interesting. Consider the least-significant digit. We can only represent $0$ or $1$ by definition. If we want to represent $2$ we have to go to a higher digit. That next-higher digit has to be able to represent the number $2$. But we can only use the symbols $1$ and $0$, so we have to agree that the second digit will be the “two’s place”:
$$ 2 * d_1 + d_0 $$Note: Here I’m using 0-based indexing despite referring to the “first” bit, and so on. I could write the “zeroth” bit, but that feels jargon-y to me.
Again, \(d_0\) and \(d_1\) can only be $0$ or $1$. So with the equation above we can represent the numbers $0$, $1$, $2$, and $3$. But what about $4$? We can do the same thing. Let’s agree that the third digit will be the “four’s” place:
$$ 4 * d_2 + 2 * d_1 + d_0 $$Each of these \(d_i\) is a weight/coefficient on the base values $1$, $2$, and $4$. Once you go to the next base value ($8$), you can start to see the pattern. Each successive base value is just the next power of two. This is exactly the same in our normal decimal system. You get up to the max digit value $9$ and then have to add another digit. We call that next digit “in the ten’s place” and it’s the first power of $10$. What happens we get max out the first two digits? We have $99$ in that case and have to add another digit, the next power of $10$, which is $100$!
If we put this all together, we see that binary numbers are really just a sequence of coefficients on the base values defined by successive powers of two:
$$ a = 2^n * d_{n} + 2^{n-1} * d_{n-1} + ... + 2^2 * d_2 + 2^1 * d_1 + 2^0 * d_0 $$Hopefully now it’s clear why I used the 0-based indexing scheme :). It’s to make this form of the “equations” nice to look at and easier to understand.
When we perform addition between two such numbers, we are adding together the individual digits (i.e. the coefficients) and carrying over any excess to the next digit.
Neve… Sometimes Be Clever!
Now comes the clever part. Let’s imagine that the highest digit (the eighth one in the Theoputer case) is not \(2^7\), but instead is \(-2^7\). Remember, we sort of just agreed on the value of that base anyway, so maybe we can get away with agreeing on a slightly different value. But it was very important before that our base value choices resulted in no missing numbers, so let’s see if that’s still the case. For simplicity, let’s consider 4-bit numbers:
| $-2^3 = -8$ | $2^2 = 4$ | $2^1 = 2$ | $2^0 = 1$ | Decimal |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | -8 |
| 1 | 0 | 0 | 1 | -7 |
| 1 | 0 | 1 | 0 | -6 |
| 1 | 0 | 1 | 1 | -5 |
| 1 | 1 | 0 | 0 | -4 |
| 1 | 1 | 0 | 1 | -3 |
| 1 | 1 | 1 | 0 | -2 |
| 1 | 1 | 1 | 1 | -1 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 2 |
| 0 | 0 | 1 | 1 | 3 |
| 0 | 1 | 0 | 0 | 4 |
| 0 | 1 | 0 | 1 | 5 |
| 0 | 1 | 1 | 0 | 6 |
| 0 | 1 | 1 | 1 | 7 |
Do some of these yourself. Here’s one:
$$ 1101_2 = (-2^3) * 1 + (2^2) * 1 + (2^1) * 0 + (2^0) * 1 = -3 $$Everything seems to work out, and there are no gaps as you can plainly see. We can’t represent the same set of numbers as we could have if we were to use positive \(2^3\), but we can represent the same number of numbers (\(2^4\) in this case).
Why do this though? Well the intuition is that when we wrote down the process of addition in the list above, we didn’t make any reference to what the bases were. We simply outlined a process for how to add a sequence of digits for any bases. Because we never wrote down special rules in the process that referred to what the actual bases are, the process we wrote down should be agnostic to them.
So let’s check! Let’s try to add $3$ and $-3$ just like we did above. $-3$ in our table is $1101$ and $3$ is $0011$, notably $3$ is the same as the binary version of $3$ and that is true (check it!) for all of the positive numbers.
1 1 0[1]
0 0 1[1]
-----------
0
(carry=1)
[1] (carry)
1 1[0]1
0 0[1]1
-----------
0 0
(carry=1)
[1] (carry)
1[1]0 1
0[0]1 1
-----------
0 0 0
(carry=1)
[1] (carry)
[1]1 0 1
[0]0 1 1
-----------
0 0 0 0
(carry=1)
Well look at that! The answer we get is $0$!… with a carry of $1$. Now you may, rightly, object! Sure, we’ve produce the value $0$ here, but what about that carry?! Well that’s a good question, so let’s unpack it.
What To Do With Carry?
If we have a carry coming from the \(2^2\) base, that means the intention is to “add \(2^3\) to the \(2^3\) digits”. That’s what we do in addition and what we all learned in grade school. Recall that the digits in this most-significant bit (MSB) represent \(-2^3\). The adder doesn’t know that, so it will plod along without taking that into account. That means the carry coming out of the \(-2^3\) base is not the same as the addition case – that was a carry coming out of a \(+2^3\) base. But again, the adder doesn’t know that! We do though, so if we can derive a meaningful and consistent way to interpret the carry coming out of the \(-2^3\) we are golden. Let’s look at the various cases that could arise:
| \(a_3\) | \(b_3\) | \(c_2\) | Decimal | \(c_3\) |
|---|---|---|---|---|
| 0 (0) | 0 (0) | 0 (0) | 0 | 0 |
| 0 (0) | 0 (0) | 1 (+8) | +8 | 0 |
| 0 (0) | 1 (-8) | 0 (0) | -8 | 0 |
| 0 (0) | 1 (-8) | 1 (+8) | 0 | 1 |
| 1 (-8) | 0 (0) | 0 (0) | -8 | 0 |
| 1 (-8) | 0 (0) | 1 (+8) | 0 | 1 |
| 1 (-8) | 1 (-8) | 0 (0) | -16 | 1 |
| 1 (-8) | 1 (-8) | 1 (+8) | -8 | 1 |
Here I’ve put the decimal equivalents in parenthesis for the various inputs to this Full Adder stage, and included the decimal output. The red rows represent cases that our numbering scheme cannot handle. As proof, look at the table above of all the numbers we can represent with this \(-2^3\) MSB base. You’ll see that $-16$ and $+8$ are not representable. That means these are the cases where our adder should indicate overflow, or in layman’s terms: “this value is not representable”.
Do you notice anything specific about those two red rows in the context of the other rows? The red rows can be determined uniquely by computing \((c_3 \; \textrm{XOR} \; c_2)\)! Our good old friend XOR! Now that’s clever.
So if we’re computing additions (and subtractions by way of negation first) using our fancy \(-2^3\) MSB base, then we can detect overflow by simply XOR’ing the last two carry bits. Let’s look at the schematic for the last two bits of the Theoputer ALU adder:
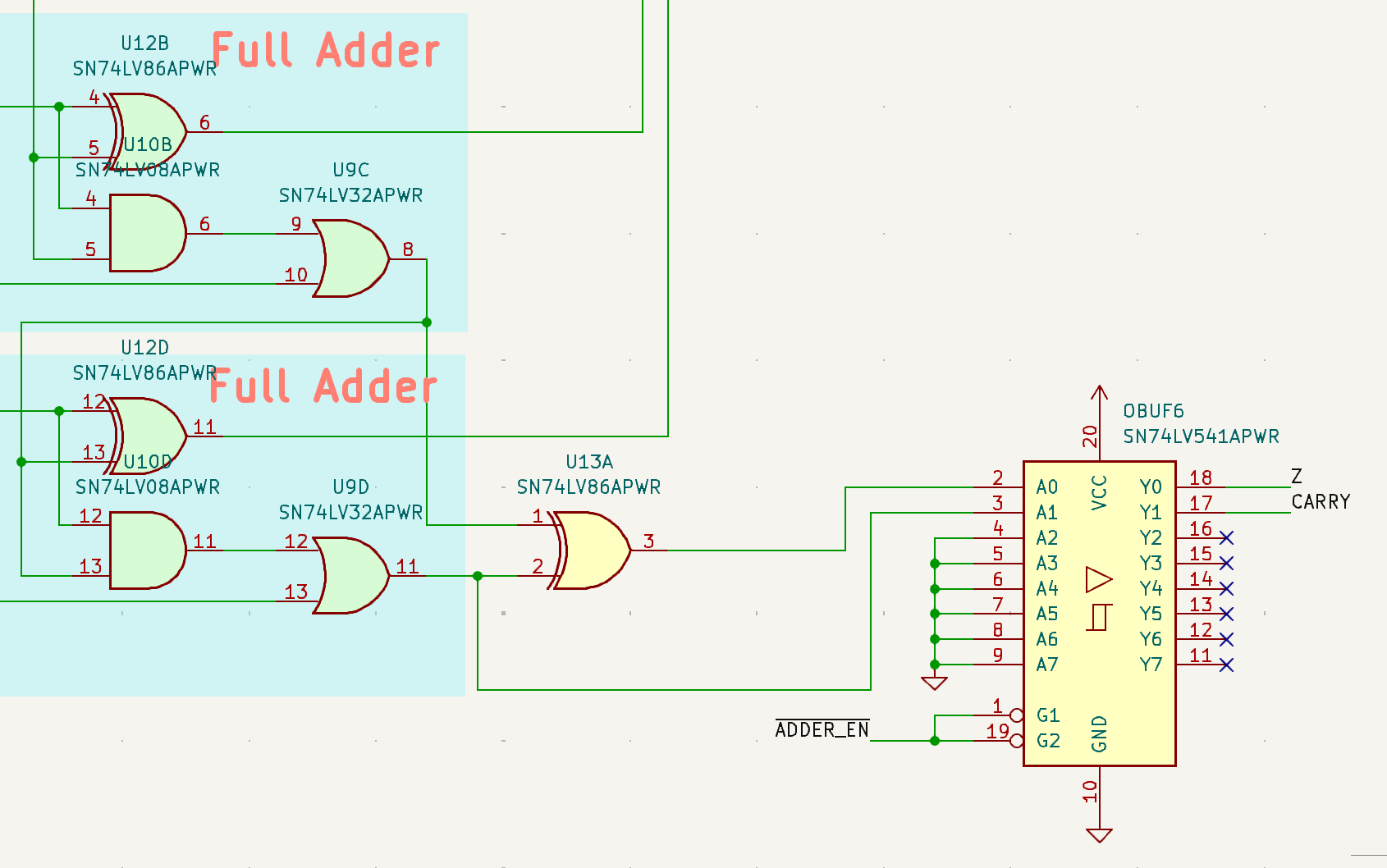
Voilà! You see very clearly the XOR there connected (via a buffer) to
the Z signal, and it is there for exactly this reason. You also
will note the regular \(c_n\) carry bit is emitted via the CARRY
signal. This is to provide flexibility in the ALU. Recall that the
adder circuit doesn’t know it’s dealing with these numbers that have
the \(2^n\) base negated. And we can use that to perform both signed
and unsigned ALU operations. We just need to, in software, look at the
Z and CARRY bits to determine whether we’ve overflowed during
signed operations or overflowed during unsigned operations.
A Fine Compliment
Ok that’s the second time I’ve intentionally misspelled that word. Enough is enough. We aren’t quite done yet. we’ve covered how to perform subtraction via two’s complement numbers, but we haven’t derived a way to take a positive number and turn it into its negative sister. So let’s do that! No one can stop us now. Consider a positive number:
$$ a = (-2^n) * 0 + 2^{n-1} * a_{n-1} + ... $$Note: The top bit will always be $0$ in a positive number in the two’s complement scheme.
We want the negative version of this number. Let’s just use a 4bit number so we can avoid using \(n\) everywhere; it will just make things easier to see:
$$ \begin{align*} a &= (-2^3) * 0 +& (2^2) * a_2 + (2^1) * a_1 + (2^0) * a_0\\ \overline{a} &= &- (2^2) * a_2 - (2^1) * a_1 - (2^0) * a_0 \end{align*} $$Now a clever part. Recall that all of the \(a_i\) are either $0$ or $1$. Let’s subtract them from one. That seems like it’s not really possible. After all, we are trying to figure out how to make a negative here to perform subtraction. But we can perform this kind of \(1 - a_i\) subtraction by negating \(a_i\) using a NOT gate. That gives us this:
$$ a^* = (-2^3) * (1) + (2^2) * (1 - a_2) + (2^1) * (1 - a_1) + (2^0) * (1 - a_0) $$Why do this? The intuition is that we need to get negatives into the equation somehow. The only way to do that naturally with logic gates is to use this kind of negation. It introduces these \(1 - a_i\) quantities, which implicitly introduces a subtraction operation via a logical operation. Let’s continue to see what we get:
$$ \begin{align*} a^* &= (-2^3) * (1) + (2^2) * (1 - a_2) + (2^1) * (1 - a_1) + (2^0) * (1 - a_0)\\ &= -8 + 4 + 2 + 1 - (2^2) * a_2 - (2^1) * a_1 - (2^0) * a_0\\ &= -1 - (2^2) * a_2 - (2^1) * a_1 - (2^0) * a_0\\ &= -1 + \overline{a} \end{align*} $$Well look at that! By doing this negation trick, to introduce some negativity through a logic gate, we found \(\overline{a} - 1\)! That means to compute \(-a\) from \(a\) we need to first invert all of the bits of \(a\) and add \(1\). Let’s check with the example for \(3_{10} = 0011_2\):
$$ \begin{align*} [0,0,1,1] &\rightarrow [\textrm{NOT}(0),\textrm{NOT}(0),\textrm{NOT}(1),\textrm{NOT}(1)] + 1\\ &= [1, 1, 0, 0] + 1\\ &= [1, 1, 0, 1]\\ &= (-2^3) * 1 + (2^2) * 1 + (2^1) * 0 + (2^0) * 1\\ &= -8 + 4 + 1\\ &= -3 \end{align*} $$And that’s awesome!
Putting It All Together
We know how to add binary numbers via Full Adders. We also know that if we do so with two’s complement numbers we can handle negative numbers. Finally, we know how to negate a number. Putting this all together, if we denote the ALU addition operation as \(f(x, y)\), then we can compute subtraction via:
$$ \begin{align*} c &= b - a\\ &= b + (-a)\\ &= f(b, [\textrm{NOT}(a_i)] + 1)\\ \end{align*} $$In the Theoputer, we will have a signal SUB (note that it’s
positive enabled) which will activate a set of NOT gates to invert one
of the ALU inputs and add $1$ before performing the normal ALU
addition covered in a prior post. But this
adding $1$ seems like it would be a wrinkle. Negating is easy
enough. We can just run the bits of the subtrahend (that’s the fancy
term for the thing you’re subtracting) through an inverter for
that. But adding $1$ seems like we might have to perform a first
addition via the ALU and then a second one to compute the real answer.
But cleverness strikes again! Recall the Full Adder circuit:
For the least signficant bit (LSB), we would just set the Cin
signal to $0$. Naturally there is no carry from the bit before the
LSB. But remember what a carry bit represents. It represents adding
one of the current base to the operation. The current base in the LSB
is the base \(2^0 = 1\). So setting Cin to $1$ in the LSB is
equivalent to adding $1$ to the operation!
Furthermore, while we can negate the subtrahend bits, we want to do so
only when SUB is high or $1$. We can perform the negation only
in this case by using our clever companion the XOR gate:
| \(a_i\) | Output | |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Notice how \(a_i\) is only inverted if the SUB signal is high. And
that is how the Theoputer ALU handles subtraction:
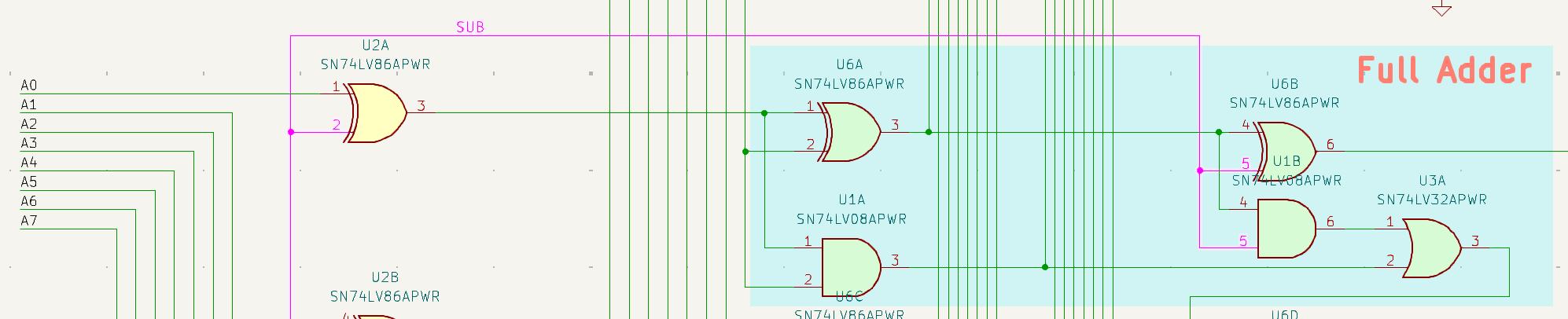
The SUB signal is highlighted and activates the XOR gate on the
individual Ai bits, while also feeding into the first Full Adder’s
Cin signal. Woohoo!