Introduction

This will be an adventure to document. I wrote the C compiler over the course of a couple of months in 2024. It was a fast-paced situation, and I wasn’t thinking about documenting my work. I do, however, have a tendency to comment my personal code quite a lot. It’s a force of habit.

So now I will try to piece things together, but be forewarned that there were a lot of things that I had to figure out that I wrote down on paper. With a pencil! And those pieces of paper are lost. And I probably forgot some of it too.

This will be the first post of several as I try to piece together the 3600 lines of code that comprise the compiler for my C(ish) language. Wish me luck.

The Parts of a Compiler

Maybe this section should be title the parts of the Cish compiler. Not all compilers are the same. Maybe if you follow the dragon book, but Cish does not. In any case, here are the two main steps of the compiling process:

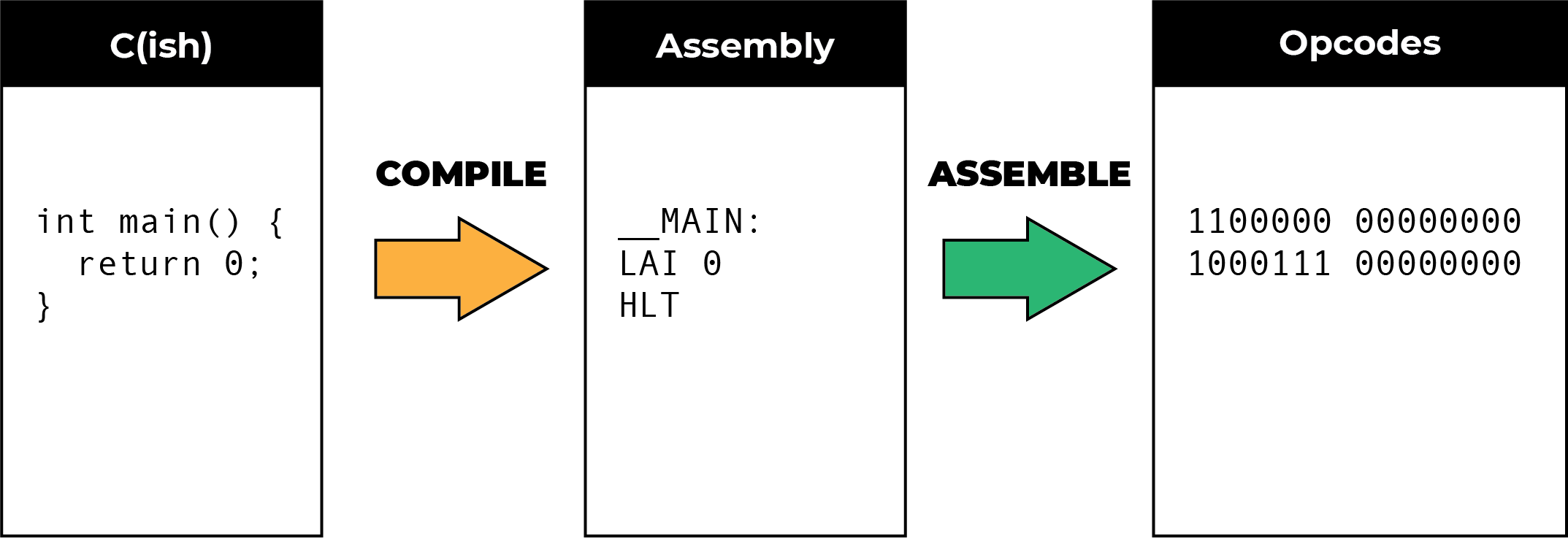
This is where some pedantry may enter the conversation because you’ll note that compilation is actually just one step in the “compiler”. This is a fairly common way to describe things though. Most people mean “compile and assemble” when they use the word “compiler”. However, these are often two distinct programs, even in many common real C compilers.

At the end of the day we need to produce a sequence of opcodes that the machine that will execute our program can understand. The set of opcodes a computer can understand is called its Instruction Set Architecture, and the Theoputer is no different. The Theoputer ISA is the only thing the Theoputer understands. It doesn’t understand C, Typescript, or English.

But it would be laborious to have to write out all of the opcodes by hand all the time. Yes you could do that. Early computers even required that. But that soon becomes not just laborious, but almost completely unmanageable.

The next-best thing to writing out opcodes is writing their shorthand versions, which are closer to a familiar language to humans. You can even see these shorthand versions in the current Theoputer ISA (column 5).

Converting from those shorthand versions to the opcodes is very straightforward, and that is the job of the assembler. You can read a lot more about the Theoputer Assembler in the dedicated post.

But once again eventually it becomes too burdensome to write out all of the assembly and manage the control flow between it. Well that’s not entirely true. There are some wizards out there who code in assembly exclusively. Especially for parts of systems that need to be heavily optimized. But it’s very uncommon and for almost all cases it is completely overkill.

Instead most programmers write and manage their programs in a “higher-level language” which gets converted into assembly and then assembled into machine code.

Why So High?

It’s worth motivating why higher level languages are so useful. After all, if you’ve read about the Theoputer Assembler you may start to think that the juice isn’t worth the squeeze for writing a full blown compiler given how simple an assembler is.

Apart from how much easier it is to follow and maintain higher-level language code, there is another critical reason for compilers: versioning.

Versioning is maybe the single most common engineering challenge out there. It rears its ugly head all over the place. And it does so even in the Theoputer.

Imagine you’ve been working hard, writing assembly programs for the Theoputer for months. Say you’ve got 10 programs that are 1000 lines of assembly code in total. Now let’s say that you’ve decided to add a new instruction to your ISA! Happy days. This new instruction is called MUL and it will multiply the contents of register A by the contents of register B. Why didn’t you have this before? Because you didn’t know it was going to be used a lot.

So you go through the process of updating the ISA, re-flashing the microcoder ROMs, and loading your new ISA into the assembler. But you’re not finished yet! You have 10 programs, each with an average of 100 lines. It’s time for you to go through all of them and update any cases where you implemented a multiply operation to use this new instruction. Oh boy. It is even worth it?!

Oh but now you’ve discovered there was a critical flaw in one of your other instructions! You have to adjust how that instruction behaves and go back through all of those programs and fix everything…

You can see where this is going. The problem here is that you’re creating new versions of the ISA, adjusting the set of instructions the computer understands, and thus necessitating a full pass over every program you’ve ever written to use the new version of the ISA.

Enter in the higher level language.

Let’s say you still have 10 programs. You still add in this new MUL instruction and subsequently find the same flaw. But what needs to change now? The programs you’ve written didn’t assume any ISA! Your compiler does, but not the programs. All you need to do is update the compiler to handle the ISA version and then recompile your programs!

And that is one of the most important reasons to use a higher-level language. This is even more acute in real computers. Imagine having to rewrite every program when a new Intel processor comes out. Or having two entirely different code bases for people who happen to have ARM64 chips and those who have AMD chips. Those will all have different ISA versions, but you will only need to adjust the compilers and recompile programs for everything to work.

In short, using a higher-level language abstracts away the details of the underlying ISA. That abstraction leads to fewer assumptions and ultimately a better overall system. Ahhhh, engineering. Yum.

The Compiler Parts

flex, yacc, and bison oh my! Those words probably mean nothing to you. They are the names of old, but still interesting ways of defining two very important parts of a compiler:

1. Lexer
2. Parser

These are fancy jargon terms. The idea behind a compiler is that we want to split compilation up into two passes (not coincidentally corresponding to the two parts):

1. Break up the program into a series of individual parts
2. Make sure the individual parts are in the correct order

Natural Language Grammar

You can think of the two operations above as how you probably understand what you’re reading right here. Consider this sentence:

“The Theoputer is awesome”

You almost certainly break that up into individual words (parts) and then you read left-to-right and understand the sentence as long as the order is correct. As a counter-example, take this sentence:

“The is awesome Theoputer”

You break that up into words, but they’re not in the correct order so you probably can discern the meaning of that sentence. Natural language isn’t the best example because the rules are not strictly adhered to, but the point remains.

How do you know that the words from the first example are in the correct order compared to the second example? Well if you’re a native English speaker/reader you probably don’t even notice that you’re actually applying the grammar rules of English as you take the words and ensure they’re in the correct order.

Loosely speaking, because natural language is not strict, English sentences are valid if they have the following grammar:

${article} ${subject} ${verb} ${adjective} ${period}

Obviously there are many other ways to make a valid English sentence, but the above is definitely one of them. If we look at the first example, we can break it into words and assign roles first via lexing:

"The" -> article
"Theoputer" -> properNoun
"is" -> verb
"awesome" -> adjective
"." -> period

Noting that a properNoun can be a subject we can see that the first sentence satisfies the grammar rule. Let’s look at the second sentence:

"The" -> article
"is" -> verb
"awesome" -> adjective
"Theoputer" -> properNoun
"." -> period

There is no grammar rule for the English language that allows the structure:

${article} ${verb} ${adjective} ${subject} ${period}

You or your first (?) grade teacher might say that the “verb has no subject” in the second example.

Machine Language

Machine languages are very similar to idealized natural languages. We also want to split the input into a series of parts and then make sure those parts adhere to the grammar of the machine language. That’s how a compiler can recognize an arbitrary string as a directive, just like you recognize the strings above as sentences.

The first step of breaking a string into parts is the job of a lexer. The parts have a special name: tokens. They probably could have been called “words” like in natural language, but they’re not.

Just like in English each token is assigned a role. Those roles are called terminals and the (token, terminal) pair is passed to the parser to see if it matches the grammar of the machine language.

Let’s take a simplified example. Imagine we have a machine language that has only one kind of statement allowed, which we’ll call variable assignment to a number. We might define the grammar of that as:

${variableType} ${variableName} ${equalsSign} ${number}

Now we need to define the tokens of this language and their corresponding terminals:

"=" -> equalsSign
"int" -> variableType
"[0-9]+" -> number
"[a-zA-Z][a-zA-Z0-9]+" -> variableName

Ok. That might look weird if you don’t know what a regular expression is. A regular expression is a language itself! That’s maybe even more confusing. But it will be extremely helpful to understand regular expressions when we look at a real machine language grammar. This post is not going to cover regular expressions, however, because they can be very complicated. Honestly, a solid Google search will be a better resource than anything else, and they are so ubiquitous that it won’t be hard to find a good explanation.

Suffice to say, [0-9] means “match any digit from 0 to 9, the + means match as many of the previous thing that’s available. So [0-9]+ means match any sequence of digits, which is all of the natural numbers. Sorry negative numbers.

[a-zA-Z] is similar, but it means to match any character between lowercase ‘a’ and uppercase ‘Z’, so the line [a-zA-Z][a-zA-Z0-9]+ means “match any sequence of numbers and letters, as long as the sequence starts with a letter”.

You’ll notice the care taken here to ensure there is no ambiguity between the number and variableName terminal definitions. Numbers must start with a digit and variables never start with a digit. That means we can always differentiate numbers from variable names.

Ok, let’s try this grammar on the following two inputs:

1. “int foo = 4”
2. “foo 4 = int”

For case (1) we have:

"int" -> variableType
"foo" -> variableName
"=" -> equalsSign
"4" -> number

That matches our grammar! If you’re very observant you may have gotten mad though. Shouldn’t int have been matches by variableName? Most lexers (maybe all?) will take the first terminal that matches in order the terminals are listed. This is necessary to allow for special keywords (like “int”) while also allowing for greater flexibility in the use of certain character sequences.

Let’s look at input (2):

"foo" -> variableName
"4" -> number
"=" -> equalsSign
"int" -> variableType

That does *not match our grammar, and thus our recognizer should say it doesn’t recognize this string. In other words, this should be a compiler error.

What Happens Next?

We now know how to split up an input program via the lexer and determine if it’s a valid program via the parser. But we haven’t generated any machine code yet and that’s all a CPU can execute.

The parser just tells us that a given program/string is valid. It doesn’t actually do the translation to machine code. However, in the process of validating the program, the parser must build something called an Abstract Syntax Tree (AST). This is similar to what we saw before when we looked at the grammar assignments:

"int" -> variableType
"foo" -> variableName
"=" -> equalsSign
"4" -> number

This isn’t a tree through. It’s just a map from terminals to grammar entities. That is due to the way we specified this particular grammar:

${variableType} ${variableName} ${equalsSign} ${number}

Real Grammars

This was all made up. Real grammars for programming languages are more rigorously defined. This is an entire field (or maybe was) of study deeply related to linguistics and early computer science foundations. As such, we will move on quickly and just note that most modern grammars are defined in something called Backus–Naur form, or more specifically Extended Backus–Naur form (EBNF).

It is not important to deeply understand what EBNF is. It is just a very common syntax for writing grammars that define programming languages.

There is a meta / recursive thing here that can be a little tricky to think through. EBNF is itself defined by a grammar. When you write a programming language grammar, you use the EBNF grammar to write the rules of the programming language grammar.

From a grammar in EBNF we can generate a parser implementation that generates an AST. The AST can be used to generate the machine code that implements the operations defined in the AST. This is all a bit too abstract now so let’s turn to an example.

Imagine we are writing the grammar for handling integer assignments in C only. Here is a grammar, in EBNF, that would handle all such programs:

grammar ExprParser;

prog:
      int_assignment EOL
      EOF
    ;

int_assignment:
      INT_KEYWORD SPC+ VARIABLE_NAME SPC+ EQUALS_SIGN SPC+ INT_LITERAL
    ;

INT_KEYWORD   : 'int';
INT_LITERAL   : [0-9]+;
EQUALS_SIGN   : '=';
VARIABLE_NAME : [A-Za-z_][A-Za-z0-9_]*;

SPC: ' ';
EOL : ';';

That might look a little intimidating at first, but it’s not too complicated. We are defining a top-level grammar rule prog and that prog will only parse strings that start with an int_assignment followed by the terminal EOL and finally by the terminal EOF. It is an annoying convention that a grammar “rule” that starts with a capital letter is assumed to be a terminal, i.e. handled by the lexer (:facepalm).

Recall that prog is the top-level rule or the root and thus if we think of the grammar as a tree, this root node has three children: int_assignment, EOL, and EOF. EOL and EOF are actually also leaf nodes because they are not parser rules. They terminate the parsing. In essence, parser rules map to non-leaf tree nodes and lexer rules map to leaf nodes.

int_assignment is a parser rule; it clearly doesn’t define a terminal. So int_assignment is a subtree in the AST that is has several children, all of which are terminals/leaf nodes: INT_KEYWORD, SPC at least once but as many times as the programmer wants, a VARIABLE_NAME, again SPCs, an EQUALS_SIGN, more SPCs, and finally an INT_LITERAL.

You’ll note the SPC+ uses the regular expression notation we discussed earlier. See! They are so ubiquitous they’re used here in the grammar definition to help parsimoniously describe terminals.

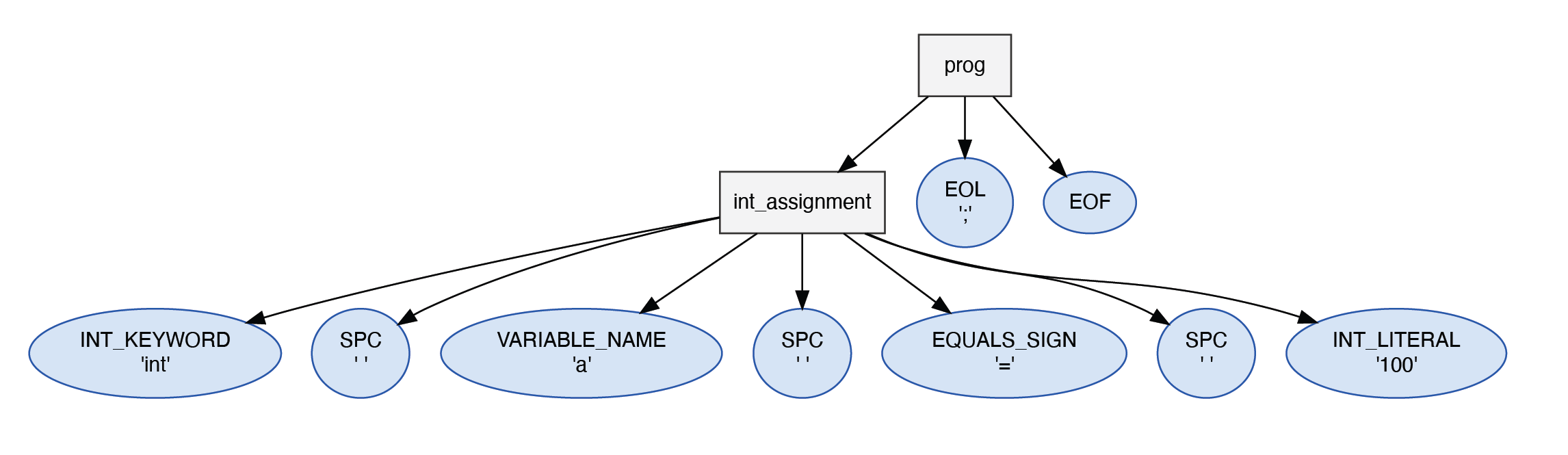
Let’s look at a program and see how the grammar above produces an AST from it:

int a = 100;

First we need to ensure this program is parse-able. All programs must have an int_assignment followed by a ; and then the end of the file. This program seems to satisfy that, but let’s break up the int_assignment. In the case above we have the string int, followed by a space, then the string a, then a space, then the string =, then a space, and finally the string 100. Sure enough we have the correct form of the int_assignment rule defined in our grammar.

Not only that, but as we went through the parsing exercise we started at the root parser rule prog and then went to the next parser rule int_assignment, collecting all of the terminals along the way. This is exactly how a tree is defined, and you could just as easily express the program above as:

Using an AST

From an AST we can build the real guts of a compiler. The AST tells us what the pieces of the program are and how they relate to each other in a very structured, hierarchical way. That AST form allows us to determine the instructions the CPU needs to perform to satisfy the AST.

In the Cish compiler, we are using a tool called ANTLR, which will take a grammar written in EBNF and create the lexer, parser, and the visitor code we need. The visitor is really a tree visitor and it just traverses the AST in depth-first order starting at the root. This is exactly what we did in written prose above.

In Cish, the compiler is written in Typescript and thus the ANTLR library is configured to take our grammar and generate the necessary code to lex, parse, and visit an input program in Typescript.

Without going into too many of the details on ANTLR, suffice it to say that the visitor that ANTLR generates provides a set of callback functions that are invoked whenever ANTLR encounters a particular node in the AST as it traverses.

Taking our example above, we would define callbacks for when ANTLR encounters the prog rule (the root), and the int_assignment rule. Note that the terminals are not rules and thus have no callbacks. They are just terminals or sequences of characters with no additional information about how they relate to other terminals or rules.

Let’s carry this further and consider what the callback for the int_assignment might look like:

visitInt_assignment(context: Int_assignmentContext): string {
  const value = Number(context.INT_LITERAL().text)
  return `LAI ${value}\n`;
}

This is what the actual callbacks look like. They are called by ANTLR with a context object that contains information about what ANTLR parsed in the rule. In this case we are extracting out one of the terminals that was lexed from this context, converting it to a number, and then returning what we want ANTLR to write out as a result of visiting this AST node. In this very contrived example we are telling ANTLR to emit the Theoputer Assembly instruction LAI ${value} which was parsed as an INT_LITERAL.

Congratulations. This is a compiler! You can see clearly that we are taking in one language (integer assignments in C) and producing instructions in another language (assembly). Remembering all the way back to the beginning of this post we can see that we have done all of the operations we need in order to call this compilation:

Tip of the Iceberg

Despite the length of this post this really just scratches the surface of the actual Cish compiler for the Theoputer. But most of the extra information is about the various and often complex callback functions like the contrived one we considered above.

It remains to be seen how deep I will ultimately go in my documentation of the compiler, because it is dense and very complex, but we shall see. Check out any of the posts with the tag ‘Compiler’ if you want to learn more.